Durchschnittsrechnung
- chevron_right 1.1 Der einfache Durchschnitt
- chevron_right 1.2 Der gewogene Durchschnitt
- chevron_right Dazu folgendes Beispiel:
Generell lässt sich mithilfe der Durchschnittsrechnung aus mehreren einzelnen Werten ein Mittelwert (= Durchschnittswert) bestimmen.
Wie genau man den Durchschnitt berechnet, wird im Folgenden gezeigt. Ihr findet an dieser Stelle die entsprechenden benötigten Formeln und auch diverse anschauliche Beispiele zum Ermitteln des Durchschnittswertes. Grundsätzlich muss bei der Durchschnittsrechnung zwischen dem einfachen Durchschnitt und dem gewogenen Durchschnitt unterschieden werden.
1.1 Der einfache Durchschnitt
Der einfache Durchschnitt wird in den meisten Fällen als Durchschnitt bzw. Mittelwert bezeichnet. Als alternative Bezeichnung wird für Durchschnitt/Mittelwert aber auch der Begriff arithmetisches Mittel verwendet.Das arithmetische Mittel liefert zu einer gegebenen Menge an gleichwertigen Zahlen bzw. Einzelwerten den zugehörigen Durchschnittswert.
Vorgehen zur Berechnung des Durchschnittswertes (Mittelwert/ arithmetisches Mittel):
Zur Berechnung des Durchschnitts addiert man zunächst alle vorliegenden Werte und teilt (dividiert) das Ergebnis anschließend durch die Gesamtanzahl der Werte. Für eine Zahlenmenge {a1, a2, ..., an} mit n Elementen lässt sich dieses Vorgehen mit folgender Formel zusammenfassen:

Beispiele für die die Berechnung vom einfachen Durchschnitt
Beispiel 1:
Der Durchschnitt der Zahlen −2, −1, 5, 6 berechnet sich zu:

Die 4 unter dem Bruchstrich findet sich dort, da der Durchschnitt aus insgesamt 4 Einzelwerten (−2, −1, 5, 6) berechnet wurde.
Wie im Beispiel zu sehen ist, gilt die Formel unabhängig vom Vorzeichen der Zahlen.
Beispiel 2: Bei einem Sportfest hat ein Speerwerfer folgende Weiten beim Wurf erreicht: 35 m; 42m; 37m und 41m.
Frage: Wie weit hat der Sportler im Durchschnitt geworfen?
Lösung:

Antwort:
Der Speerwerfer hat im Mittel somit 38, 75m weit geworfen.
Anschauliche Darstellung:
Das arithmetische Mittel lässt sich mithilfe von Gewichten veranschaulichen. Zunächst stellt man sich dazu ein Brett vor, von dessen Mitte aus ein Zahlenstrahl bei 0 beginnend nach rechts (ins Positive) und nach links (ins Negative) aufgetragen ist. Auf diese Leiste werden nun identische Gegenstände gleicher Masse an die jeweiligen Stellen der gegebenen Zahlenwerte platziert. Das arithmetische Mittel der Zahlen liefert dann genau die Stelle des Schwerpunkts der Leiste. D.h. die Stelle, an der man das Brett abstützen kann, ohne, dass sich der linke oder rechte Teil nach oben oder unten bewegt – also den austarierten Gleichgewichtszustand – ist genau die Stelle des arithmetischen Mittels.
1.2 Der gewogene Durchschnitt
Der gewogene Durchschnitt (auch gewichteter Durchschnitt/Mittelwert oder gewogenes/ gewichtetes arithmetisches Mittel genannt) wird dann angewandt, wenn Einzelwerte mit unterschiedlicher Gewichtung an einem Gesamtwert beteiligt sind. Werden z. B. unterschiedliche Artikel oder Sorten zu jeweils verschiedenen Mengen in der Berechnung mit einbezogen, so müssen sie entsprechend ihrem Anteil unterschiedlich gewichtet oder gewogen werden.
Zur Berechnung des gewichteten arithmetischen Mittels:
Um das gewichtete arithmetische Mittel zu berechnen, werden zunächst die Einzelwerte {x1, x2, ..., xn} mit ihrer Gewichtung {g1, g2, ..., gn} addiert. Diese Produkte aller gegebenen Elemente samt ihrer Gewichtung müssen dann addiert werden. Die so ermittelte Summe ist schließlich noch durch die Anzahl n aller Elemente zu teilen (dividieren).
Dazu folgendes Beispiel:
Karl kauft 1 Pullover für 50 € und 1 Pullover für 100 €. Im Schnitt kostet dann jeder Pullover 75 €. Auch, wenn er je 10 Pullover für 50 € und 100 € kauft. Was aber passiert, wenn er 2 Pullover für 50 € und 3 Pullover für einen Preis von 100 € kauft? In diesem Fall reicht es nicht mehr aus, die Preise und die Anzahl der Pullover zu addieren. Man muss die Produkte aus der Anzahl der Pullover und den dazugehörigen Preisen addieren und diese Summe durch die Anzahl der Pullover teilen. D.h. statt dem arithmetischen Mittel ist das gewichtete arithmetische Mittel zu bestimmen. Die Rechnung sieht dann wie folgt aus:
Summe der Produkte der Elemente (Preis · Anzahl)
2 · 50 = 100
3 · 100 = 300
100 + 300 = 400
Summe der der Elemente:
2 + 3 = 5
gewichtetes arithmetisches Mittel:
400 : 5 = 80
Falls Karl also 2 Pullover zu 50 € und 3 Pullover zu 100 € kauft, kostet ihn eine Hose im Schnitt 80 €, da die teureren Pullover, von denen er mehr kauft als von den billigeren Pullovern, mehr ins Gewicht fallen.
Die Formel zur Berechnung des gewichteten arithmetischen Mittels:

Das in der Formel verwendete Zeichen Ø (durchgestrichener Kreis) ist das Symbol für das gewichtete arithmetische Mittel. Die x-Werte repräsentieren die Anzahl der gegebenen Elemente, das g den Faktor, mit dem das entsprechende Element gewichtet wird.
Im Beispiel mit Karl:
x1 = 2 Pullover, g1 = 50 € usw..
Wer nur ungern abstrakte Formeln lernt, der kann sich auch folgenden inhaltlichen Zusammenhang einprägen:

Angewendet auf die Beispielaufgabe ergibt sich diese Rechnung: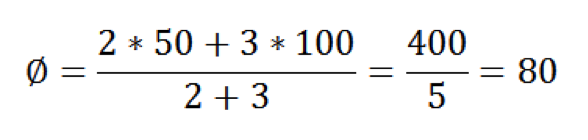
whatshot Beliebteste Artikel
- chevron_right Buchungssätze Übungsaufgaben
- chevron_right Übungsaufgaben
- chevron_right Kaufmännisches Rechnen
- chevron_right Verteilungsrechnung
- chevron_right Deckungsbeitragsrechnung Übung
- chevron_right Anlagegüter (Verkauf) buchen
- chevron_right Bilanz Muster
- chevron_right Differenzbesteuerung
- chevron_right Aufwendungen für Rohstoffe
- chevron_right Buchungssatz
category Auch in dieser Kategorie
- chevron_right Verteilungsrechnung
- chevron_right Durchschnitt berechnen
- chevron_right Dreisatz
- chevron_right Prozentrechnung im Hundert
- chevron_right Prozentrechnung auf Hundert
- chevron_right Dreisatz (ungerades Verhältnis)
- chevron_right Dreisatz Rechner
- chevron_right Zusammengesetzer Dreisatz