Mischkosten – Variable Kosten - Fixkosten

---

Zunächst beantworten wir eine ganz einfache Frage:

Wie ist der Begriff Mischkosten zusammengesetzt? Aus den Begriffen Misch(ung) und Kosten.
Der Begriff Misch(ung) lässt schon erahnen, dass es hier um eine Vermischung von Kosten bzw. Kostenarten geht, nämlich von fixen und variablen Kosten.

Wir klären nun (zur Wiederholung) die Begrifflichkeit von fixen bzw. Fix- und variablen Kosten .

• Fixkosten: Diese Kosten entstehen unabhängig von der produzierten Stückzahl.
  Beispiele:
  
  • Personalkosten von festangestellten Mitarbeitern
  • Grundgebühren, etwa für Strom
  • Abschreibungen, etwa für Gebäude und Maschinen
• Variable Kosten: Diese Kosten entstehen abhängig von der produzierten Stückzahl.
  Beispiele:
  
  • Materialkosten (Roh- oder Hilfsstoffe)
  • Stromkosten für die tatsächliche Maschinenlaufzeit
  • Fremdleistungskosten (z.B. es wird ein Teil außerhalb des Unternehmens gefertigt, dann fallen auch nur für das eine Teil Kosten an. Werden fünf Teile extern gefer-tigt, fallen die Kosten eben für fünf dieser Teile an, usw.)
  • Personalkosten von Mitarbeitern, deren Leistung über Zeitarbeitsfirmen in An-spruch genommen werden kann. Achtung Mitarbeiter, die befristete Arbeitsverträ-ge haben (z.B. 3 Monate) werden als abbaubare fixe Kosten bezeichnet, da diese Kosten eben für die Zeit des Vertrages (hier 3 Monate) entstehen und für diese Zeit fix sind.

Nun gibt es eine Reihe von Kostenarten, die sowohl fixe als auch variable Kostenanteile enthalten. Wenn es also erfüllt ist, dass eine Kostenart fixe und variable Kostenbestandteile enthält, dann werden diese als Mischkosten bezeichnet.

2. Beispiel zu Mischkosten

Das Unternehmen DJ-Metalery stellt Stahlrohre für den Bau von Brücken und den Hochhaus-bau her. Die Produkte werden international vermarktet.

Zur Produktion dieser Stahlrohre werden in der Abteilung A zwei Spezialroboter benötigt. Zur Einstellung, Überwachung und Wartung der Roboter ist ein -Industriemeister IHK- fest eingestellt, für den Personalkosten inklusiv der Arbeitgeberanteile zur Sozialversicherung (AG Anteil zur SV) in Höhe von 4.000,00 Euro anfallen. Außerdem ist an jedem Roboter ein Industriemechaniker tätig, für den jeweils Personalkosten inklusiv der Arbeitgeberanteile zur Sozialversicherung in Höhe von 3.200,00 Euro entstehen. Ein Roboter hat einen Stromver-brauch von 800 Kilowatt pro Stunde. Eine Kilowattstunde kostet 0,25 Euro.

Der Stromanbieter Greenpower-Energy berechnet dem Unternehmen eine monatliche Grundgebühr in Höhe von 151,26 Euro für die permanente Bereitstellung des Kraftstroms. 1m² Stahlblech (Stahl-blech ist ein Rohstoff) kostet im Einkauf 8,82 Euro. Spezielle Klebstoffe (Klebstoff ist ein Hilfsstoff) werden in der Produktion pro Meter Stahlrohr für 5,50 Euro benötigt.

Wir schlüsseln nun die Kosten nach variablen und fixen Kosten auf

• Fixkosten

  Meistergehalt	4.200,00 Euro
  Gesellengehalt	6.400,00 Euro
  Grundgebühr Strom	151,26 Euro

• Variable Kosten

  Kilowattstunde Strom	0,25 Euro
  Spezialklebstoff pro Meter	5,50 Euro
  1m² Stahlblech	8,52 Euro

• Mischkosten

Als Mischkosten können hier die Kosten für den Strom verstanden werden, denn die Bereit-stellungsgebühr i.H.v. 151,26 Euro ist fix und die Kosten pro Kilowattstunde sind i.H.v. 0,25 Euro variabel.

3. Rechenbeispiele in Anknüpfung

• Roboter 1

1. Dieser Roboter produziert 5 Meter Rohre.
2. Die Rohre haben einen Durchmesser (D) von 64 cm. Demnach beträgt der Radi-us (R) 32 cm, denn dieser berechnet sich nach folgender Formel #
   
   

   	Durchmesser
   Radius =	----------------
   	2

3. Die Produktion eines Meterstückes (1 Meter Rohr) dauert 10 Minuten.
4. Die Rohre müssen mit 5 Lagen Stahlblech ummantelt werden.

3.1 Berechnung der variablen Kosten

Welche variablen Kosten entstehen für die Produktion von einem 5 Meter Rohr?

3.2 Berechnung der Materialkosten

1m² Stahlblech kostet 8,52 Euro. Nun müssen wir berechnen, wieviel Stahlblech wir benötigen. Um das herauszufinden, brauchen wird die mathematische Formel für die Bestimmung der Mantelfläche eines Zylinders.



Die Formel zur Berechnung der Mangeloberfläche lautet wie folgt:

Mantelfläche = 2 ⋅ π ⋅ r ⋅ h

Nun setzen wir die Werte ein
Mantelfläche = 2 ⋅ π ⋅ Radius des Rohres ⋅ Höhe des Rohres
Mantelfläche = 2 ⋅ π ⋅ 0,64 Meter/2 ⋅ 5 Meter
Hinweis: 0,64 /2 = Durchmesser des Rohres / 2 = Radius des Rohres - π ≈ 3,14

Mantelfläche ≈ 10, 05 m²

Nun haben wir die Mantelfläche durch einfaches Einsetzen von Werten in eine Formel bestimmt und arbeiten mit diesem Wert weiter.

Gemäß Aufgabenstellung muss das Rohr fünffach ummantelt werden, also multi-plizieren wir die Mantelfläche mit der Anzahl der Ummantelungen und erhalten damit den Materialbedarf für ein 5 Meter Rohr, sowie die daraus resultierenden Materialkosten.

Materialbedarf = Mantelfläche ⋅ 5 = 10,05 m² ⋅ 5 = 50,25 m² Stahlblech

1 Meter Stahlblech kostet 8,52 Euro, damit kosten 50,25 m² 428,13 Euro.
Rechnung: 50,25 m² ⋅ 8,52 Euro = 428,13 Euro für das Stahlblech.

Zu den Kosten des Stahlbleches kommen laut Aufgabestellung die Kosten für den Spezialklebstoff i.H.v. 5,50 Euro pro Meter.
Damit ergeben sich für den Spezialklebstoff Kosten i.H.v.
5,50 Euro pro Meter ⋅ 5 Meter = 25,25 Euro
Die gesamten Materialkosten belaufen sich damit auf

1. Kosten für Stahlblech	428,13 Euro
2. +Kosten für Spezialklebstoff	25,25 Euro
________________________________	___________
3. Gesamte Materialkosten	453,38 Euro

3.3 Berechnung der Energiekosten

Wir wissen:

• Der Roboter hat laut Aufgabenstellung einen Energieverbrauch von 800 Kilowatt pro Stunde (kw/h)
• Eine Kilowattstunde kostet 0,25 Euro
• Die Produktion eines 1-Meter-Rohres dauert 10 Minuten.

I. Wir berechnen die Stromkosten pro Stunde:

Preis pro Kilowattstunde ⋅ 800 Kilowatt = Strompreis pro Stunde für den Roboter 1

0,25 Euro ⋅800 Kilowatt = 200 Euro Stromkosten bei 800 Kilowatt Stromver-brauch pro Stunde.

Nun wissen wir, dass für eine Stunde Laufzeit des Roboters Stromkosten in Höhe von 200 Euro anfallen.

II. Wir berechnen nun die Stromkosten für 50 Minuten Fertigungszeit

Laut Aufgabenstellung benötigt der Roboter 10 Minuten, um einen Meter Rohr zu fertigen. Da unser Rohr 5 Meter lang ist, müssen wir zunächst die Ferti-gungszeit einfach mit 5 multiplizieren, es ergeben sich dann folgende Werte:

1 Meter = 10 Minuten → 5 Meter = 50 Minuten

(Simple Rechnung: 10 Minuten pro Meter ⋅ 5 Meter = 50 Minuten)

Aus der obigen Rechnung (I) wissen wir, dass für eine Stunde 200 Euro Stromkosten anfallen.

Eine Stunde entspricht 60 Minuten, die entsprechend 200 Euro kosten

3.4 Berechnung der gesamten variablen Kosten

Aus dem ersten Punkt „Berechnung der Materialkosten“ wissen wir, dass für ein fünf Meter langes Rohr Materialkosten i.H.v. 453,38 Euro anfallen.
Aus dem zweiten Punkt „Berechnung der Energiekosten“ wissen wir, dass für ein fünf Meter langes Rohr Energiekosten i.H.v. 166,67 Euro anfallen.

Um nun die gesamten variablen Kosten zu bestimmen, addieren wir einfach die beiden o.a. Werte!

a) Materialkosten	453,38 Euro
b) + Energiekosten	166,67 Euro
________________________________	___________
c) Σ Variable Stück Kosten	620,05 Euro

4. Berechnung der fixen (Stück)Kosten

Bei der Berechnung der fixen Stückkosten wird es interessant, denn die Höhe der fixen Stückkosten hängt eben davon ab, wieviel Stück produziert werden.
Wir fassen die Fixkosten zusammen

a) Meistergehalt	4.000,00 Euro
b) Gehalt Zweier Industriemechaniker	6.400,00 Euro
c) Grundgebühr Stromanbieter	151,26 Euro
________________________________	___________
d) Fixe Kosten	10.551,26 Euro

Wir rufen uns an dieser Stelle ins Gedächtnis, dass 2 Roboter in der Abteilung A betrieben werden. Nun unterstellen wir in unserer weiteren Betrachtung, dass der Meister an Roboter 1 genauso viel Zeit verbringt, wie an Roboter 2. Auch unter-stellen wir, dass ein Industriemechaniker an Roboter 1 arbeitet und der andere an Roboter 2. Schlussendlich wird unterstellt, dass die beiden Roboter den gleichen Stromverbrauch haben und auch die gleiche Anzahl an Stunden im Monat laufen, damit ergibt sich für Roboter 1 die folgende Fixkostensituation.

a) Meistergehalt	2.000,00 Euro
b) Gehalt Industriemechaniker	3.200,00 Euro
c) Grundgebühr Stromanbieter	75,63 Euro
________________________________	___________
d) Fixe Kosten	5.275,63 Euro

Würde in dem hier betrachteten Monat (Gehälter und Grundgebühr werden i.d.R. monatlich gezahlt) nur 1 einziges Rohr produziert werden, wäre das ein sehr teures Roh, denn das eine Rohr müsste die gesamten Fixkosten „tragen“. Unter Punkt 4 e) weiter unten im Text wird auf den Verlauf der fixen Stückkosten nochmals nä-her eingegangen.

5. Berechnung der Gesamtkosten

a) Σ Variable Stück Kosten	620,05 Euro
b) + Fixe Kosten	5.275,63 Euro
________________________________	___________
c) Gesamtkosten pro Rohr, wenn nur 1 Rohr produziert würde	5895,68 Euro

Die hier angeführte Rechnung ist mit absoluter Vorsicht zu betrachten, denn sie gilt nur dann, wenn nur 1 Stück (5-Meterrohr) produziert werden würde. Würden 2 Stück (5-Meterrohr) produziert werden, würde sich folgende Kostensituation er-geben.

d) Σ Variable Stück Kosten	620,05 Euro	620,05 Euro
e) + Fixe Stückkosten	5.275,63 Euro / 2	2637,82 Euro
________________________________	___________	___________
f) Gesamtkosten bei 2 Rohren	-,--	3257,87 Euro

Auf die fixen Stückkosten sowie deren Entwicklung wird unter Punkt 4 e) weiter unten im Text nochmal vertieft eingegangen.
Im Folgenden werden die Kostenverläufe aller Kostenarten übersichtlich darge-stellt.

6. Darstellung der Kostenverläufe

6.1 Verlauf der Fixkosten

Stückzahl	1	100	200	300	400	500
Fixe Kosten	5.275,63 €	5.275,63 €	5.275,63 €	5.275,63 €	5.275,63 €	5.275,63 €

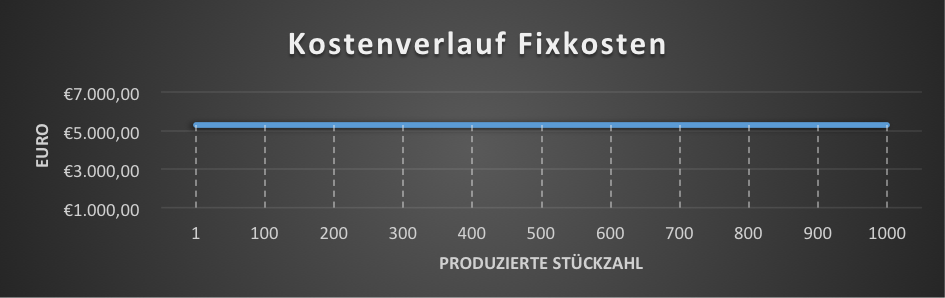
Wie aus dem Diagramm unschwer zu erkennen ist, ist es für die Fixkosten irrelevant bzw. egal, wieviel Stück (5-Meter Rohre) produziert werden. Ob 1 Stück oder ob 1.000 Stück pro-duziert werden, die fixen Kosten betragen immer 5.275,63 €.
Merke: Es geht hier nicht um die fixen Stückkosten, diese werden unter Punkt 4 e) vertieft betrachtet.

6.2 Verlauf der variable Kosten

Stückzahl	1	100	200	300	400	500
Variable Kosten	620,05 €	62.005,00 €	124.010,00 €	186.015,00 €	248.020,00 €	310.025,00 €

 

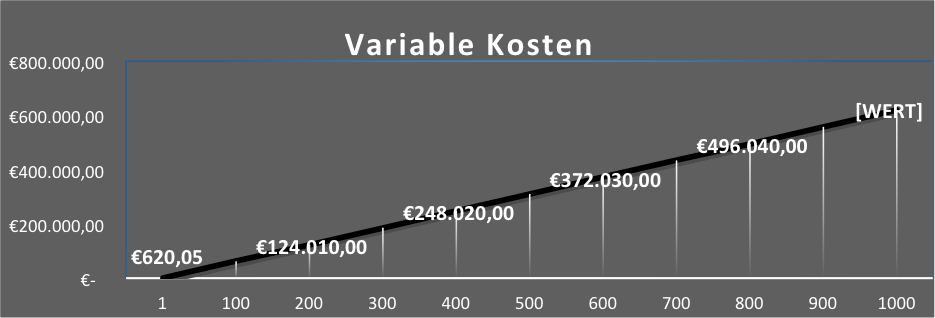
Anhand des Diagrammes kann problemlos nachvollzogen werden, dass die variablen Kosten in Abhängigkeit der Produktionsmenge steigen. Produziere ich nur 1 5-Meter-Rohr, entstehen eben nur variable Kosten i.H.v. 620,05 Euro für das eine Rohr, produziere ich aber 1000 5 Meter Rohre, entstehen auch die tausendfachen Materialkosten, nämlich 620.050,00 Euro.

6.3 Verlauf der Gesamtkosten

Stückzahl	1	100	200	300	400	500
Gesamte Stückkosten	5.895,68 €	62.057,76 €	124.036,38 €	186.032,59 €	248.033,19 €	310.035,55 €

Dieses Diagramm ist annähernd identisch, mit der Kostenverlaufsdarstellung der variablen Kosten. Es erklärt sich von selbst, dass die Gesamtkosten, die variablen und fixen Kosten ent-halten. Im Vergleich zu Abbildung 2 subtrahiert man im aktuellen Diagramm den Fixkosten-anteil von 5.275,63 Euro und man erhält die identischen Werte, wie in Abbildung 3.

Beispiel:
Für 1.000 Stück fallen Gesamtkosten i.H.v. 625.325,63 Euro an. Subtrahiert man davon den Fixkostenanteil 5.275,63, erhält man den variablen Kostenanteil i.H.v. 620.050,00 €.
Rechnung

Gesamtkosten	635.325,63
- Fixkostenanteil	5.275,63
________________________	____________
Variabler Kostenanteil	620.050,00

Hinweis:
In der Literatur findet sich häufig die folgende Gleichung i n Bezug auf die Gesamtkosten

G(x) = Kvar(x) +Kfix

Diese Gleichung bedeutet nichts anderes, als

Gesamtkosten = Variable-Kosten + Fixkosten

Gesamtkosten = Variable Kosten⋅ (produzierte Stückzahl) + Fixkosten

Beispiel in Anlehnung an das oben angeführte einfache Beispiel:

635.325,63 = 620,50 ⋅ (1.000) + 5.275,63

6.4 Verlauf der Mischkosten

Weiterhin können wir untersuchen, wie sich die Mischkosten in Abhängigkeit der produzier-ten Stückzahl verhalten. Wie in der Einführung beschrieben, gilt, dass die Mischkosten einen variablen und einen fixen Kostenanteil haben. Wir können daher folgende Gleichung aufstel-len.

Gesamte Mischkosten = Variabler Mischkostenanteil⋅ (produzierte Stückzahl) + Fixer Mischkostenanteil

In unserem Beispiel hatten wir als Mischkosten die Stromkosten identifiziert, weil diese sich aus einem fixen Kostenbestandteil, nämlich der Grundgebühr i.H.v. 151,26 Euro und einem variablen Kostenbestandteil, nämlich dem Preis pro Kilowattstunde i.H.v. 0,25 Euro zusam-mensetzen. Wir haben in unserer Rechnung zu den variablen Kosten ermittelt, dass für ein 5 Meter Rohr Energiekosten i.H.v. 166,67 Euro entstehen.
Würden wir diese beiden Zahlen in einem Diagramm abbilden, würde dieses wie folgt ausse-hen

6.5 Verlauf der fixen Stückkosten

In der folgenden Übersicht wird dargestellt, wie sich die fixen Stückkosten in Abhängig-keit der produzierten Menge verhalten. Es geht also darum, welchen Fixkostenanteil jedes produzierte Stück (5 Meter Rohr) zu tragen hat.

Stückzahl	1	2	3	4	5
Fixe Stückkosten	5.275,63 €	2.637,82 €	1.758,54 €	1.318,91 €	1.055,13 €

Aus dem Diagramm und der Tabelle erkennen wir, dass die fixen Stückkosten mit jeder zu-sätzlich produzierten Einheit (5 Meter¬ ¬Rohr) sinken. Das ist auch logisch, denn wenn nur ein Stück (5 Meter Rohr) produziert wird, dann muss dieses Stück allein die gesamten Fixkosten tragen. Werden aber 2 Stück produziert, dann sinken die fixen Stückkosten bereits von 5.275,63 € auf 2.637,82 €, weil die Fixkosten durch 2 dividiert werden. Werden nun 3, 4 oder sogar 1.000 5 Meter Rohre produziert, dann werden die gesamten Fixkosten durch die produ-zierte Stückzahl geteilt. Aus diesem Wissen können wir nun die folgende einfache Formel ableiten

	Gesamte Fixkosten
Fixe Stückkosten	-----------------------------------------------
	Gesamten produzierte Stückzahlen

Nochmal zur Kontrolle am Beispiel, dass nur zwei Rohre produziert werden würden

	5275,63
2.637,82 =	-----------------
	2

Anmerkung & Weiterführende Informationen: Die Abnahme der fixen Stückkosten gilt im-mer bis zur Auslastung der Kapazitätsgrenze. Sollte sich die DJ-Metalery dazu entschlie-ßen, in der Abteilung einen weiteren Roboter bereitzuhalten der die 5-Meter-Rohre produ-ziert, welcher nach Auslastung des hier im Beispiel betrachteten Roboters eingeschaltet wird, steigen natürlich die fixen Stückkosten wieder, weil für zwei Roboter entsprechende Kosten anfallen. In diesem Falle spricht man von sprungfixen Kosten .

6.6 Verlauf der Gesamtkosten pro Stück

Wir haben im Abschnitt „c) Verlauf der Gesamtkosten“ gelernt, dass für die Ermittlung der Gesamtkosten folgende Formel gilt

G(x) = Kvar(x) +Kfix

bzw.

Gesamtkosten = Variabler Kostenanteil pro Stück ⋅ (produzierte Stückzahl) + Fixkostenanteil

Wenn wir jetzt an den letzten Abschnitt e) denken, wird es sofort deutlich, dass man die Gesamtkosten pro Stückkosten dann wie folgt ermittelt

	Gesamtkosten
Gesamtkosten pro Stück =	------------------------------------
	Gesamte produzierte Stückzahl

In Bezug auf die Formel zur Berechnung der fixen Stückkosten unter Abschnitt e) sollte es logisch erscheinen, dass auch die Gesamtkosten pro Stück mit zunehmender Menge abneh-men, weil auch die in den Gesamtkosten enthaltenen Fixkosten pro Stück gem. Abbildung 5 mit zunehmender Menge sinken.

Die nachfolgende Abbildung stellt die Abnahme der Gesamtkosten pro Stück anschaulich dar

Stückzahl	1	2	3	4	5
Gesamtkos-ten /Stück	5.895,68 €	3.257,87 €	2.378,59 €	1.938,96 €	1.675,18 €

Sie können die Zahlen kontrollieren, indem Sie einfach die variablen Stückkosten i.H.v. 620,05 Euro subtrahieren, dann werden Sie die fixen Stückkosten errechnen, wie diese unter Abbildung 5 dargestellt sind.

7. Zusammenfassung

Fixkosten: Dieser Kostenanteil ist unabhängig von der produzierten Menge. Es ist egal, ob wir mit Hilfe des Roboters 1 Stück 5-Meter-Rohr produzieren oder ob wir 1.000 Stück 5 Meter Rohr produzieren. Die Kosten für den festangestellten Industriemechaniker, sowie die Hälfte des Meistergehaltes, der für beide Roboter zuständig ist und die Hälfte der Grund-gebühr für den Strom fällt immer an.



Variable Kosten: Dieser Kostenanteil ist abhängig von der produzierten Menge. Wenn wir ein 5 Meter Rohr produzieren, entstehen Kosten für Material und Strom (das sind variable Kos-ten) von 620,05 Euro, für zwei 5-Meter-Rohre entstehen Kosten für Material und Strom von 1.240,10 Euro, für drei 5-Meter-Rohre entstehen Kosten für Material und Strom von 1.860,15 Euro usw.



Mischkosten: Diese Kostenart besteht aus zwei Kostenkomponenten, nämlich einem Fixkos-ten- und einem variablen Kostenanteil. Beispiele dafür wären z.B. die Stromkosten, hier exis-tiert ein Fixkostenanteil -die Grundgebühr- und einen variablen Kostenanteil -der Preis für die Kilowattstunde-.

Gesamtkosten: Die Gesamtkosten ist die Summe aus variablen und fixen Kosten. Für die Be-rechnung der Gesamtkosten gilt die folgende Formel

Gesamtkosten = Variabler Kostenanteil pro Stück ⋅ (produzierte Stückzahl) + Fixkostenanteil

Fixe Stückkosten: Anhand der fixen Stückkosten ist ersichtlich, welchen Fixkostenanteil ein produziertes Stück tragen muss. Für die Berechnung der fixen Stückkosten gilt die folgende Formel

	Gesamtkosten
Fixe Stückkosten =	-------------------------------------------
	Gesamte produzierte Stückzahl

Gesamtkosten pro Stück: Wie der Name schon sagt, zeigen die Gesamtkosten pro Stück an, welche Gesamtkosten pro Stück (in Abhängigkeit der Produktionsmenge) entstehen. Für die Berechnung der Gesamtkosten pro Stück gilt die folgende Formel

	Gesamtkosten
Gesamtkosten pro Stück =	------------------------------------
	Gesamte produzierte Stückzahl

Alternativ gilt die folgende Formel

	Fixkosten
Gesamtkosten pro Stück = Variabler Kostenanteil pro Stück +	-----------------------------------------------
	Gesamte produzierte Stückzahl

---